大学入学共通テスト（情報） 過去問
令和5年度（2023年度）追・再試験
問38 (＜旧課程＞情報関係基礎（第3問） 問7)
問題文
次の文章を読み、問いに答えよ。
ある個別指導塾では、午後の時間帯を、第1時限から第5時限までの五つの時限に分けて講義を開講している。受講生は時限を指定して、指導を受ける。
時限ごとに受講生数をまとめたところ、第1時限から順に10、8、19、14、7（人）となった。この個別指導塾では、一対一での指導を行っている。そのため、講義を開講するには、この受講生数と同じ人数の講師を各時限に割り当てる必要がある。
講師は、複数の時限の講義を連続して担当することがある。そこで、塾の講師割り当て担当者は、講師の人数を担当開始時限・終了時限ごとにまとめた担当表を作成することにした。
はじめに、各講師が一つの時限のみを担当する場合を考え、表3の担当表を作成した。これは、表の開始時限と終了時限が等しい要素（以下、対角要素と呼ぶ。）に、各時限の受講生数と同じ講師人数を記したものである。表の合計値が58であることから、その日に出勤して講義を担当する講師の人数が58人であることがわかる。なお、以下では担当表の「開始時限k，終了時限s」の要素を【k，s】と表記する。
ここでは3時限以上連続で担当する場合について考えていく。
例えば、第2時限から第4時限まで3時限連続で担当する講師をn人設定する場合、【2，4】にnを記したうえで、表3の網掛けで示した人数8、19、14をnずつ減らすことになる。
ここで、【2，4】に設定できる人数の上限について考える。【2，4】にnを設定するには、網掛けで示した人数をnずつ減らす必要があるが、担当表には負の人数は記せない。そのため、【2，4】に設定できる人数の上限は、表3の網掛けで示した「該当する対角要素」の最小値である8となる。
以下、【k，s】に設定できる人数の上限を【k，s】に記し、担当表を書き換える操作を【k，s】に着目した集約と呼ぶ。表3に対して、【2，4】に着目した集約を行った後の担当表は表4になる。
【k，s】に着目した集約を行う手続きを作成していくうえでは、まず【k，s】に設定できる人数の上限を求める必要がある。そこで、ある時限帯（開始時限～終了時限）に対応する「該当する対角要素」の最小値を求める手続き（図2）を作成した。この手続きでは、開始時限をhajime、終了時限をowariに格納して時限帯を指定すると、2次元配列Hyouを参照し、最小値をsaisyouに格納する。なお、最小値を求めるうえでは、まずHyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている。その後、対角要素のowari番目までに格納された値について、順番にsaisyouと比較している。
表3の初期状態の担当表の人数が2次元配列Hyouに格納されている状態で、図2の手続きを実行し、開始時限に1、終了時限に5を入力したとき、（06）行目の処理は（ サ ）回実行される。
（ キ ）にあてはまるものを1つ選べ。
ある個別指導塾では、午後の時間帯を、第1時限から第5時限までの五つの時限に分けて講義を開講している。受講生は時限を指定して、指導を受ける。
時限ごとに受講生数をまとめたところ、第1時限から順に10、8、19、14、7（人）となった。この個別指導塾では、一対一での指導を行っている。そのため、講義を開講するには、この受講生数と同じ人数の講師を各時限に割り当てる必要がある。
講師は、複数の時限の講義を連続して担当することがある。そこで、塾の講師割り当て担当者は、講師の人数を担当開始時限・終了時限ごとにまとめた担当表を作成することにした。
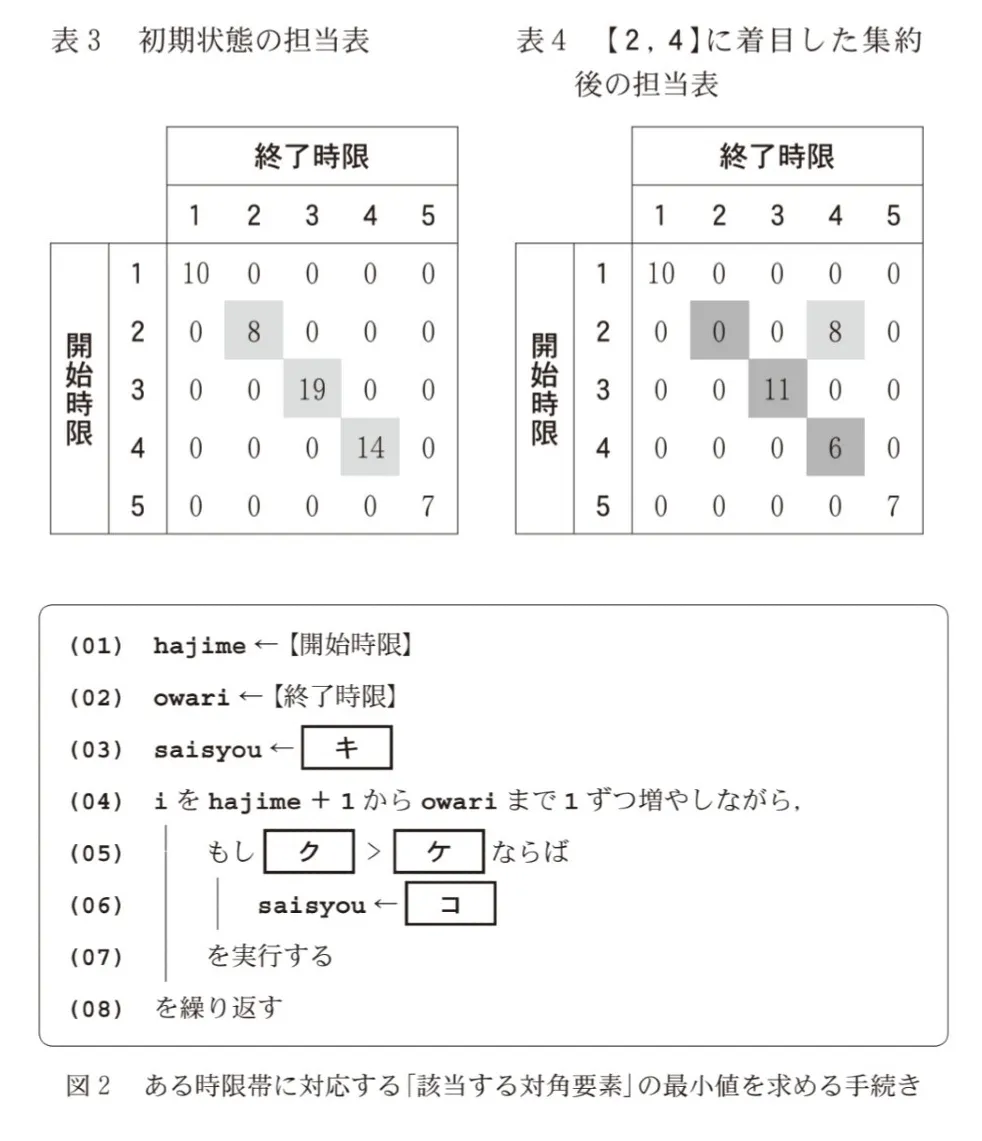
はじめに、各講師が一つの時限のみを担当する場合を考え、表3の担当表を作成した。これは、表の開始時限と終了時限が等しい要素（以下、対角要素と呼ぶ。）に、各時限の受講生数と同じ講師人数を記したものである。表の合計値が58であることから、その日に出勤して講義を担当する講師の人数が58人であることがわかる。なお、以下では担当表の「開始時限k，終了時限s」の要素を【k，s】と表記する。
ここでは3時限以上連続で担当する場合について考えていく。
例えば、第2時限から第4時限まで3時限連続で担当する講師をn人設定する場合、【2，4】にnを記したうえで、表3の網掛けで示した人数8、19、14をnずつ減らすことになる。
ここで、【2，4】に設定できる人数の上限について考える。【2，4】にnを設定するには、網掛けで示した人数をnずつ減らす必要があるが、担当表には負の人数は記せない。そのため、【2，4】に設定できる人数の上限は、表3の網掛けで示した「該当する対角要素」の最小値である8となる。
以下、【k，s】に設定できる人数の上限を【k，s】に記し、担当表を書き換える操作を【k，s】に着目した集約と呼ぶ。表3に対して、【2，4】に着目した集約を行った後の担当表は表4になる。
【k，s】に着目した集約を行う手続きを作成していくうえでは、まず【k，s】に設定できる人数の上限を求める必要がある。そこで、ある時限帯（開始時限～終了時限）に対応する「該当する対角要素」の最小値を求める手続き（図2）を作成した。この手続きでは、開始時限をhajime、終了時限をowariに格納して時限帯を指定すると、2次元配列Hyouを参照し、最小値をsaisyouに格納する。なお、最小値を求めるうえでは、まずHyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている。その後、対角要素のowari番目までに格納された値について、順番にsaisyouと比較している。
表3の初期状態の担当表の人数が2次元配列Hyouに格納されている状態で、図2の手続きを実行し、開始時限に1、終了時限に5を入力したとき、（06）行目の処理は（ サ ）回実行される。
（ キ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
大学入学共通テスト（情報）試験 令和5年度（2023年度）追・再試験 問38（＜旧課程＞情報関係基礎（第3問） 問7） （訂正依頼・報告はこちら）
次の文章を読み、問いに答えよ。
ある個別指導塾では、午後の時間帯を、第1時限から第5時限までの五つの時限に分けて講義を開講している。受講生は時限を指定して、指導を受ける。
時限ごとに受講生数をまとめたところ、第1時限から順に10、8、19、14、7（人）となった。この個別指導塾では、一対一での指導を行っている。そのため、講義を開講するには、この受講生数と同じ人数の講師を各時限に割り当てる必要がある。
講師は、複数の時限の講義を連続して担当することがある。そこで、塾の講師割り当て担当者は、講師の人数を担当開始時限・終了時限ごとにまとめた担当表を作成することにした。
はじめに、各講師が一つの時限のみを担当する場合を考え、表3の担当表を作成した。これは、表の開始時限と終了時限が等しい要素（以下、対角要素と呼ぶ。）に、各時限の受講生数と同じ講師人数を記したものである。表の合計値が58であることから、その日に出勤して講義を担当する講師の人数が58人であることがわかる。なお、以下では担当表の「開始時限k，終了時限s」の要素を【k，s】と表記する。
ここでは3時限以上連続で担当する場合について考えていく。
例えば、第2時限から第4時限まで3時限連続で担当する講師をn人設定する場合、【2，4】にnを記したうえで、表3の網掛けで示した人数8、19、14をnずつ減らすことになる。
ここで、【2，4】に設定できる人数の上限について考える。【2，4】にnを設定するには、網掛けで示した人数をnずつ減らす必要があるが、担当表には負の人数は記せない。そのため、【2，4】に設定できる人数の上限は、表3の網掛けで示した「該当する対角要素」の最小値である8となる。
以下、【k，s】に設定できる人数の上限を【k，s】に記し、担当表を書き換える操作を【k，s】に着目した集約と呼ぶ。表3に対して、【2，4】に着目した集約を行った後の担当表は表4になる。
【k，s】に着目した集約を行う手続きを作成していくうえでは、まず【k，s】に設定できる人数の上限を求める必要がある。そこで、ある時限帯（開始時限～終了時限）に対応する「該当する対角要素」の最小値を求める手続き（図2）を作成した。この手続きでは、開始時限をhajime、終了時限をowariに格納して時限帯を指定すると、2次元配列Hyouを参照し、最小値をsaisyouに格納する。なお、最小値を求めるうえでは、まずHyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている。その後、対角要素のowari番目までに格納された値について、順番にsaisyouと比較している。
表3の初期状態の担当表の人数が2次元配列Hyouに格納されている状態で、図2の手続きを実行し、開始時限に1、終了時限に5を入力したとき、（06）行目の処理は（ サ ）回実行される。
（ キ ）にあてはまるものを1つ選べ。
ある個別指導塾では、午後の時間帯を、第1時限から第5時限までの五つの時限に分けて講義を開講している。受講生は時限を指定して、指導を受ける。
時限ごとに受講生数をまとめたところ、第1時限から順に10、8、19、14、7（人）となった。この個別指導塾では、一対一での指導を行っている。そのため、講義を開講するには、この受講生数と同じ人数の講師を各時限に割り当てる必要がある。
講師は、複数の時限の講義を連続して担当することがある。そこで、塾の講師割り当て担当者は、講師の人数を担当開始時限・終了時限ごとにまとめた担当表を作成することにした。
はじめに、各講師が一つの時限のみを担当する場合を考え、表3の担当表を作成した。これは、表の開始時限と終了時限が等しい要素（以下、対角要素と呼ぶ。）に、各時限の受講生数と同じ講師人数を記したものである。表の合計値が58であることから、その日に出勤して講義を担当する講師の人数が58人であることがわかる。なお、以下では担当表の「開始時限k，終了時限s」の要素を【k，s】と表記する。
ここでは3時限以上連続で担当する場合について考えていく。
例えば、第2時限から第4時限まで3時限連続で担当する講師をn人設定する場合、【2，4】にnを記したうえで、表3の網掛けで示した人数8、19、14をnずつ減らすことになる。
ここで、【2，4】に設定できる人数の上限について考える。【2，4】にnを設定するには、網掛けで示した人数をnずつ減らす必要があるが、担当表には負の人数は記せない。そのため、【2，4】に設定できる人数の上限は、表3の網掛けで示した「該当する対角要素」の最小値である8となる。
以下、【k，s】に設定できる人数の上限を【k，s】に記し、担当表を書き換える操作を【k，s】に着目した集約と呼ぶ。表3に対して、【2，4】に着目した集約を行った後の担当表は表4になる。
【k，s】に着目した集約を行う手続きを作成していくうえでは、まず【k，s】に設定できる人数の上限を求める必要がある。そこで、ある時限帯（開始時限～終了時限）に対応する「該当する対角要素」の最小値を求める手続き（図2）を作成した。この手続きでは、開始時限をhajime、終了時限をowariに格納して時限帯を指定すると、2次元配列Hyouを参照し、最小値をsaisyouに格納する。なお、最小値を求めるうえでは、まずHyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている。その後、対角要素のowari番目までに格納された値について、順番にsaisyouと比較している。
表3の初期状態の担当表の人数が2次元配列Hyouに格納されている状態で、図2の手続きを実行し、開始時限に1、終了時限に5を入力したとき、（06）行目の処理は（ サ ）回実行される。
（ キ ）にあてはまるものを1つ選べ。
- 0
- hajime
- owari
- saisyou
- i
- Hyou［hajime，hajime］
- Hyou［hajime，owari］
- Hyou［owari，owari］
- Hyou［hajime，i］
- Hyou［i，i］
- Hyou［i，owari］
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
図2の手続きでは、（01）〜（03）行目で3つの変数に対して、それぞれの初期値を格納しています。
そして、ここで問われている空欄「キ」には、変数saisyouに格納される初期値を示す内容が入ります。
また、問題文を読むと変数saisyouの初期値については、2つの記載があります。
「2次元配列Hyouを参照し、最小値をsaisyouに格納する」
「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」
これはつまり、表3の対角要素の中から、指定した開始時限の講師数を変数saisyouの初期値としてまず格納する、という意味です。
問題文に記載された2つの条件と矛盾しないように、選択肢を選びましょう。
問題文には「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」とありますが、表3を見ると5つの対角要素には10・8・19・14・7という値があらかじめ入っています。
どれを初期値に指定しても、saisyouの初期値が0になることはありません。
問題文には「2次元配列Hyouを参照し、最小値をsaisyouに格納する」とありますが、変数hajimeは講義の開始時限を示すもので、表3の対角要素の値ではありません。
問題文には「2次元配列Hyouを参照し、最小値をsaisyouに格納する」とありますが、変数owariは講義の終了時限を示すものであって、表3の対角要素の値ではありません。
変数saisyouに同じ変数saisyouの値を格納する、という処理を行っても何も変わらないため、この選択肢は間違いです。
変数iは（04）〜（08）行目の処理を繰り返す際のカウンターとして使われるもので、表3の対角要素ではありません。
問題文には「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」とあります。
また、変数hajimeには2時限連続で講義を担当する講師の開始時限を格納する、と（01）行目で定義されています。
そして2次元配列Hyou[k,s]のうち、対角要素のhajime番目に当たるのは、Hyou[hajime,hajime]です。
つまり、この選択肢が正解となります。
2次元配列Hyou[hajime,owari]は、2時間連続で担当する講師の人数を示すものです。
担当講義の開始時間と終了時間が異なる可能性もあるため、「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」という問題文の記述と矛盾するので、間違いであるとわかります。
2次元配列Hyou[owari,owari]は、変数saisyouと一番最後に比較される対角要素であり、saisyouの初期値ではありません。
（04）行目を見ると、変数iの初期値はhajime＋1とわかります。
問題文には「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」と書かれているのに、Hyou[hajime,hajime＋1]は対角要素になりませんから、間違いとわかります。
（04）行目を見ると、変数iの初期値はhajime＋1とわかります。
するとHyou[i,i]はHyouの対角要素のうち、hajime番目の次ということになり、問題文に書かれた「Hyouの対角要素のhajime番目に格納された値をsaisyouの初期値としている」という内容と矛盾します。
従って、この選択肢は間違いだとわかります。
この問いでは講師が3時限以上連続で担当する場合もあるため、変数iの初期値であるhajime＋1の値と、owariの値が異なる場合もあり得ます。
すると2次元配列Hyou[hajime＋1,owari]が対角要素にならないため、この選択肢は間違いであるとわかります。
参考になった数0
この解説の修正を提案する
前の問題（問37）へ
令和5年度（2023年度）追・再試験 問題一覧
次の問題（問39）へ