大学入学共通テスト(情報) 過去問
令和5年度(2023年度)追・再試験
問13 (<旧課程>情報関係基礎(第1問) 問13)
問題文
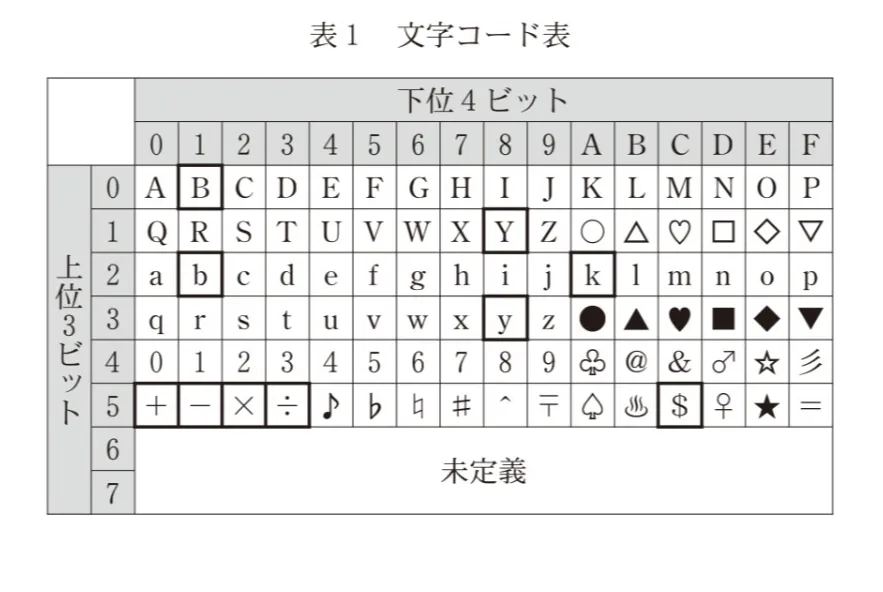
表1に示す文字コード表について考える。この文字コード表では、英数字や記号に対して7ビットで構成される文字コードを割り当てている。行の見出しは文字コードの上位3ビットを、列の見出しは文字コードの下位4ビットを16進表記で示している。例えば文字「k」の場合、上位3ビットは2、下位4ビットはAであることから、文字「k」に対する文字コードは16進表記で2Aとなり、2進表記では0101010となる。これをふまえると、2進表記の文字コード0000010で表される文字は( セ )であり、文字「$」に対する2進表記の文字コードは( ソ )となる。
この文字コード表では、四則演算を表す「+」、「−」、「✕」、「÷」の位置関係から、2進表記で表現した( タ )ことがわかっていれば、これらの演算子のいずれかであることがわかる。また、文字「B」と「b」や文字「Y」と「y」など、同じアルファベットの大文字と小文字の文字コードには、( チ )という関係がある。
( ソ )にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(情報)試験 令和5年度(2023年度)追・再試験 問13(<旧課程>情報関係基礎(第1問) 問13) (訂正依頼・報告はこちら)
表1に示す文字コード表について考える。この文字コード表では、英数字や記号に対して7ビットで構成される文字コードを割り当てている。行の見出しは文字コードの上位3ビットを、列の見出しは文字コードの下位4ビットを16進表記で示している。例えば文字「k」の場合、上位3ビットは2、下位4ビットはAであることから、文字「k」に対する文字コードは16進表記で2Aとなり、2進表記では0101010となる。これをふまえると、2進表記の文字コード0000010で表される文字は( セ )であり、文字「$」に対する2進表記の文字コードは( ソ )となる。
この文字コード表では、四則演算を表す「+」、「−」、「✕」、「÷」の位置関係から、2進表記で表現した( タ )ことがわかっていれば、これらの演算子のいずれかであることがわかる。また、文字「B」と「b」や文字「Y」と「y」など、同じアルファベットの大文字と小文字の文字コードには、( チ )という関係がある。
( ソ )にあてはまるものを1つ選べ。

- 111011
- 110001
- 100001
- 111111
- 1100001
- 1011001
- 1010110
- 1011100
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
正解は「 1011100」です。
表1から、文字「$」に対する16進表記の文字コードは5C(上位3ビットが5、下位4ビットがC)と分かります。
16進表記から2進表記への変換は、10進表記に変換してから考えると分かりやすいです。
・5
5は10進表記でも5です。
2進表記への変換は、5を2で割り続けて、商が1以下になるまでのそれぞれの余りを使います。
5÷2=2・・・1
2÷2=1・・・0
一番最後の商と、それぞれの余りを逆から並べると2進表記になり、101です。
・C
Cは10進表記で12です。
2進表記への変換は、12を2で割り続けて、商が1以下になるまでのそれぞれの余りを使います。
12÷2=6・・・0
6÷2=3・・・0
3÷2=1・・・1
一番最後の商と、それぞれの余りを逆から並べると2進表記になり、1100です。
よって、2進表記の文字コードは「 1011100」(上位3ビットが101、下位4ビットが1100)です。
参考になった数0
この解説の修正を提案する
前の問題(問12)へ
令和5年度(2023年度)追・再試験 問題一覧
次の問題(問14)へ