共通テスト（情報） 過去問
令和6年度（2024年度）本試験
問26 (＜旧課程＞情報関係基礎（第2問） 問8)
問題文
次の文章を読み、問いに答えよ。
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A～Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
トウ星とカイ星がどちらもトウカイ銀河にあることを知ったMさんは、これを利用すれば質問回数を減らせないかと思い、次のグループ法を考えた。
＜グループ法＞
手順1 「トウカイ銀河から来ましたか？」と質問し、返答が「はい」なら手順2、「いいえ」なら手順3に進む。
手順2 「トウ星人ですか？」と質問し、返答が「はい」ならトウ星人、「いいえ」ならカイ星人である。
手順3 「ホク星人ですか？」と質問し、返答が「はい」ならホク星人、「いいえ」ならリク星人である。
グループ法で表1の宇宙船Aの人に出身星をたずねると、10人全員への合計質問回数は（ キク ）回になる。グループ法では、宇宙船A～Eのどの10人に出身星をたずねても、合計質問回数は同じになる。
Mさんは、質問回数をできる限り減らすには、順次法（出身星のみを質問する方法）やグループ法をどう使うとよいか考えてみた。
順次法を使うなら、出身者が多い星から順番に質問した場合に、合計質問回数が最小になる。宇宙船Aの10人全員に順次法で出身星をたずねるときの合計質問回数の最小は（ ケコ ）回である。また、それぞれの宇宙船について、順次法のうち合計質問回数が最小となる順番でたずねると、5隻の中で合計質問回数が最も少ないのは（ サ ）である。
では、順次法とグループ法は、どう使い分けるべきだろうか。順次法を使うと、グループ法を使うときと比べて、ある人たちへの質問回数は多くなり、またある人たちへの質問回数は少なくなる。前者（順次法で質問回数が多くなる）の人数が後者（少なくなる）の人数を上回る場合は、順次法のうち質問回数が最小となる順番でたずねても、グループ法を使うときと比べて合計質問回数が多くなる。つまり、（ シ ）の人数と（ ス ）の人数の合計が、（ セ ）の人数より多い場合は、グループ法を使う方が効率的だということになる。ただ、実際に出身星をたずねるときにこのような検討はできないので、順次法やグループ法を的確に使って質問回数を減らすことは難しいとMさんは感じた。
（ サ ）にあてはまるものを1つ選べ。
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A～Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
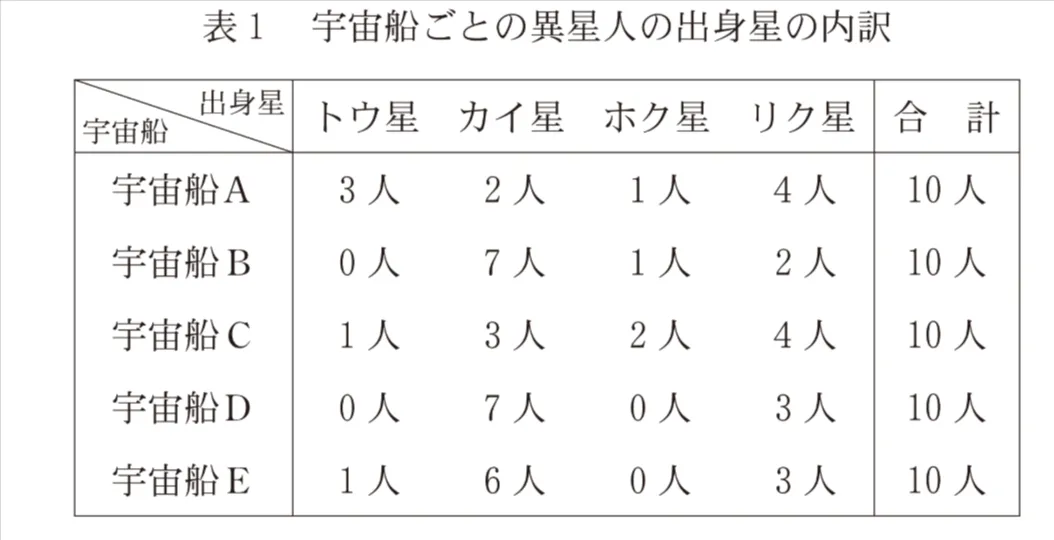
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
トウ星とカイ星がどちらもトウカイ銀河にあることを知ったMさんは、これを利用すれば質問回数を減らせないかと思い、次のグループ法を考えた。
＜グループ法＞
手順1 「トウカイ銀河から来ましたか？」と質問し、返答が「はい」なら手順2、「いいえ」なら手順3に進む。
手順2 「トウ星人ですか？」と質問し、返答が「はい」ならトウ星人、「いいえ」ならカイ星人である。
手順3 「ホク星人ですか？」と質問し、返答が「はい」ならホク星人、「いいえ」ならリク星人である。
グループ法で表1の宇宙船Aの人に出身星をたずねると、10人全員への合計質問回数は（ キク ）回になる。グループ法では、宇宙船A～Eのどの10人に出身星をたずねても、合計質問回数は同じになる。
Mさんは、質問回数をできる限り減らすには、順次法（出身星のみを質問する方法）やグループ法をどう使うとよいか考えてみた。
順次法を使うなら、出身者が多い星から順番に質問した場合に、合計質問回数が最小になる。宇宙船Aの10人全員に順次法で出身星をたずねるときの合計質問回数の最小は（ ケコ ）回である。また、それぞれの宇宙船について、順次法のうち合計質問回数が最小となる順番でたずねると、5隻の中で合計質問回数が最も少ないのは（ サ ）である。
では、順次法とグループ法は、どう使い分けるべきだろうか。順次法を使うと、グループ法を使うときと比べて、ある人たちへの質問回数は多くなり、またある人たちへの質問回数は少なくなる。前者（順次法で質問回数が多くなる）の人数が後者（少なくなる）の人数を上回る場合は、順次法のうち質問回数が最小となる順番でたずねても、グループ法を使うときと比べて合計質問回数が多くなる。つまり、（ シ ）の人数と（ ス ）の人数の合計が、（ セ ）の人数より多い場合は、グループ法を使う方が効率的だということになる。ただ、実際に出身星をたずねるときにこのような検討はできないので、順次法やグループ法を的確に使って質問回数を減らすことは難しいとMさんは感じた。
（ サ ）にあてはまるものを1つ選べ。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
共通テスト（情報）試験 令和6年度（2024年度）本試験 問26（＜旧課程＞情報関係基礎（第2問） 問8） （訂正依頼・報告はこちら）
次の文章を読み、問いに答えよ。
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A～Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
トウ星とカイ星がどちらもトウカイ銀河にあることを知ったMさんは、これを利用すれば質問回数を減らせないかと思い、次のグループ法を考えた。
＜グループ法＞
手順1 「トウカイ銀河から来ましたか？」と質問し、返答が「はい」なら手順2、「いいえ」なら手順3に進む。
手順2 「トウ星人ですか？」と質問し、返答が「はい」ならトウ星人、「いいえ」ならカイ星人である。
手順3 「ホク星人ですか？」と質問し、返答が「はい」ならホク星人、「いいえ」ならリク星人である。
グループ法で表1の宇宙船Aの人に出身星をたずねると、10人全員への合計質問回数は（ キク ）回になる。グループ法では、宇宙船A～Eのどの10人に出身星をたずねても、合計質問回数は同じになる。
Mさんは、質問回数をできる限り減らすには、順次法（出身星のみを質問する方法）やグループ法をどう使うとよいか考えてみた。
順次法を使うなら、出身者が多い星から順番に質問した場合に、合計質問回数が最小になる。宇宙船Aの10人全員に順次法で出身星をたずねるときの合計質問回数の最小は（ ケコ ）回である。また、それぞれの宇宙船について、順次法のうち合計質問回数が最小となる順番でたずねると、5隻の中で合計質問回数が最も少ないのは（ サ ）である。
では、順次法とグループ法は、どう使い分けるべきだろうか。順次法を使うと、グループ法を使うときと比べて、ある人たちへの質問回数は多くなり、またある人たちへの質問回数は少なくなる。前者（順次法で質問回数が多くなる）の人数が後者（少なくなる）の人数を上回る場合は、順次法のうち質問回数が最小となる順番でたずねても、グループ法を使うときと比べて合計質問回数が多くなる。つまり、（ シ ）の人数と（ ス ）の人数の合計が、（ セ ）の人数より多い場合は、グループ法を使う方が効率的だということになる。ただ、実際に出身星をたずねるときにこのような検討はできないので、順次法やグループ法を的確に使って質問回数を減らすことは難しいとMさんは感じた。
（ サ ）にあてはまるものを1つ選べ。
ついに異星人が地球を訪れた。しかも一度に、トウ星、カイ星、ホク星、リク星という、四つもの星から。
異星人は計50人で、10人ずつに分かれて5隻の宇宙船A～Eに乗って訪れた。Mさんは地球人代表として、異星人の方々に出身星、つまりどの星から来たのかをたずねた。異星人はMさんの質問を理解できた。しかしMさんには、異星人の返答は「はい」と「いいえ」しかわからなかったため、全員の出身星をたずねるのにかなり手間取ってしまった。
異星人の出身星をたずねた結果は、次の表1のとおりであった。Mさんは、今後異星人が訪れたときに備えて、どのようにすれば効率よく全員の出身星をたずねることができたのかを考えることにした。
トウ星とカイ星がどちらもトウカイ銀河にあることを知ったMさんは、これを利用すれば質問回数を減らせないかと思い、次のグループ法を考えた。
＜グループ法＞
手順1 「トウカイ銀河から来ましたか？」と質問し、返答が「はい」なら手順2、「いいえ」なら手順3に進む。
手順2 「トウ星人ですか？」と質問し、返答が「はい」ならトウ星人、「いいえ」ならカイ星人である。
手順3 「ホク星人ですか？」と質問し、返答が「はい」ならホク星人、「いいえ」ならリク星人である。
グループ法で表1の宇宙船Aの人に出身星をたずねると、10人全員への合計質問回数は（ キク ）回になる。グループ法では、宇宙船A～Eのどの10人に出身星をたずねても、合計質問回数は同じになる。
Mさんは、質問回数をできる限り減らすには、順次法（出身星のみを質問する方法）やグループ法をどう使うとよいか考えてみた。
順次法を使うなら、出身者が多い星から順番に質問した場合に、合計質問回数が最小になる。宇宙船Aの10人全員に順次法で出身星をたずねるときの合計質問回数の最小は（ ケコ ）回である。また、それぞれの宇宙船について、順次法のうち合計質問回数が最小となる順番でたずねると、5隻の中で合計質問回数が最も少ないのは（ サ ）である。
では、順次法とグループ法は、どう使い分けるべきだろうか。順次法を使うと、グループ法を使うときと比べて、ある人たちへの質問回数は多くなり、またある人たちへの質問回数は少なくなる。前者（順次法で質問回数が多くなる）の人数が後者（少なくなる）の人数を上回る場合は、順次法のうち質問回数が最小となる順番でたずねても、グループ法を使うときと比べて合計質問回数が多くなる。つまり、（ シ ）の人数と（ ス ）の人数の合計が、（ セ ）の人数より多い場合は、グループ法を使う方が効率的だということになる。ただ、実際に出身星をたずねるときにこのような検討はできないので、順次法やグループ法を的確に使って質問回数を減らすことは難しいとMさんは感じた。
（ サ ）にあてはまるものを1つ選べ。
- 宇宙船A
- 宇宙船B
- 宇宙船C
- 宇宙船D
- 宇宙船E
正解！素晴らしいです
残念...
この過去問の解説 （3件）
01
宇宙船Ａ～宇宙船Ｅの５隻の宇宙船に乗った宇宙人の出身星について、順次方による合計質問回数について考察しています。
順次法の場合は、出身者が多い星の宇宙人には質問回数が少ない方が全体の合計質問回数が少なくなるという観点から、５隻の各船について、出身者数が多い順で並べてその質問回数を表にすると以下のようになります。
上記の表を見ながら、各船の１０人全員の合計質問回数を求めると、
・宇宙船Ａ
１×４＋２×３＋３×２＋３×１＝４＋６＋６＋３＝１９(回)
・宇宙船Ｂ
１×７＋２×２＋３×１＋３×０＝７＋４＋３＋０＝１４(回)
・宇宙船Ｃ
１×４＋２×３＋３×２＋３×１＝４＋６＋６＋３＝１９(回)
・宇宙船Ｄ
１×７＋２×３＋３×０＋３×０＝７＋６＋０＋０＝１３(回)
・宇宙船Ｅ
１×６＋２×３＋３×１＋３×０＝６＋６＋３＋０＝１５(回)
これより、５隻の船の中で合計質問回数が最も少ないのは、宇宙船Ｄの「１３回」です。
以上より、解答欄(サ)には、「宇宙船Ｄ」の選択肢の番号が入ります。
簡単な計算の繰り返しですが、間違わないようにしましょう！
参考になった数0
この解説の修正を提案する
02
順次法を使うとき、出身者が多い星から順番に質問した場合、質問回数は、
出身者が1番目に多い星：質問回数1回
出身者が2番目に多い星：質問回数2回
出身者が3番目に多い星：質問回数3回
出身者が4番目に多い星：質問回数3回
となることが分かります。
宇宙船Bを出身者が多い星から順番に並べて質問回数を求めます。
カイ星：7人×1回＝7
リク星：2人×2回＝4
ホク星：1人×3回＝3
トウ星：0人×3回＝0
7+4+3+0＝14
宇宙船Bの合計質問回数の最小は14回です。
宇宙船Cを出身者が多い星から順番に並べて質問回数を求めます。
リク星：4人×1回＝4
カイ星：3人×2回＝6
ホク星：2人×3回＝6
トウ星：1人×3回＝3
4+6+6+3＝19
宇宙船Cの合計質問回数の最小は19回です。
宇宙船Dを出身者が多い星から順番に並べて質問回数を求めます。
カイ星：7人×1回＝7
リク星：3人×2回＝6
トウ星：0人×3回＝0
ホク星：0人×3回＝0
7+6+0+0＝13
宇宙船Dの合計質問回数の最小は13回です。
宇宙船Eを出身者が多い星から順番に並べて質問回数を求めます。
カイ星：6人×1回＝6
リク星：3人×2回＝6
トウ星：1人×3回＝3
ホク星：0人×3回＝0
6+6+3+0＝15
宇宙船Eの合計質問回数の最小は15回です。
5隻の中で合計質問回数が最も少ないのはサ宇宙船Dです。
参考になった数0
この解説の修正を提案する
03
正解は「宇宙船D」です。
(1)宇宙船Aはの出身星構成は、以下の通りです（表1より）。
リク星人：4人
トウ星人：3人
ホク星人：1人
カイ星人：2人
元の質問方法での1人あたりの質問回数は以下の通りです。
リク星人：1回
トウ星人：2回
ホク星人：3回
カイ星人：3回
宇宙船Aの質問回数の合計は4×1+2×3+1×3+3×2=4+6+3+6=19回
(2)宇宙船Bはの出身星構成は、以下の通りです（表1より）。
カイ星人：7人
リク星人：2人
トウ星人：1人
ホク星人：0人
元の質問方法での1人あたりの質問回数は以下の通りです。
カイ星人：1回
リク星人：2回
トウ星人：3回
ホク星人：3回
宇宙船Bの質問回数の合計は7×1+2×2+1×3+0×3=7+4+2=14回
となります。
(3)宇宙船Cはの出身星構成は、以下の通りです（表1より）。
カイ星人：4人
リク星人：3人
トウ星人：2人
ホク星人：1人
元の質問方法での1人あたりの質問回数は以下の通りです。
カイ星人：1回
リク星人：2回
トウ星人：3回
ホク星人：3回
宇宙船Cの質問回数の合計は4×1+3×2+2×3+1×3=4+6+6+3=19回
となります。
(4)宇宙船Dはの出身星構成は、以下の通りです（表1より）。
カイ星人：7人
リク星人：3人
トウ星人：0人
ホク星人：0人
元の質問方法での1人あたりの質問回数は以下の通りです。
カイ星人：1回
リク星人：2回
トウ星人：3回
ホク星人：3回
宇宙船Dの質問回数の合計は7×1+3×2+0×3+0×3=7+6=13回
となります。
(5)宇宙船Eはの出身星構成は、以下の通りです（表1より）。
カイ星人：6人
リク星人：3人
トウ星人：1人
ホク星人：0人
元の質問方法での1人あたりの質問回数は以下の通りです。
カイ星人：1回
リク星人：2回
トウ星人：3回
ホク星人：3回
宇宙船Eの質問回数の合計は6×1+3×2+1×3+0×3=6+6+=15回
となります。
(1)~(5)より、順次法のうち合計質問回数が最小となる順番でたずねると、5隻の中で合計質問回数が最も少ないのは宇宙船Dの13回となります。
参考になった数0
この解説の修正を提案する
前の問題（問25）へ
令和6年度（2024年度）本試験 問題一覧
次の問題（問27）へ