大学入学共通テスト(情報) 過去問
令和4年度(2022年度)本試験
問80 (<旧課程>情報関係基礎(第4問) 問20)
問題文
この競技を4人で競い合っている。各選手は他3人の選手と50試合(先攻25試合、後攻25試合)ずつ合計150試合、全体では300試合を行い、勝率により順位を決定する。勝率は、引き分けを除いた試合数で勝ち数を割って計算する。
次の文章を読み、空欄( ナ )に入れるのに最も適当なものを、後の解答群のうちから一つ選べ。なお、以下の問題を解答するにあたっては、使用する表計算ソフトウェアの説明(リンク) を参照するとよい。
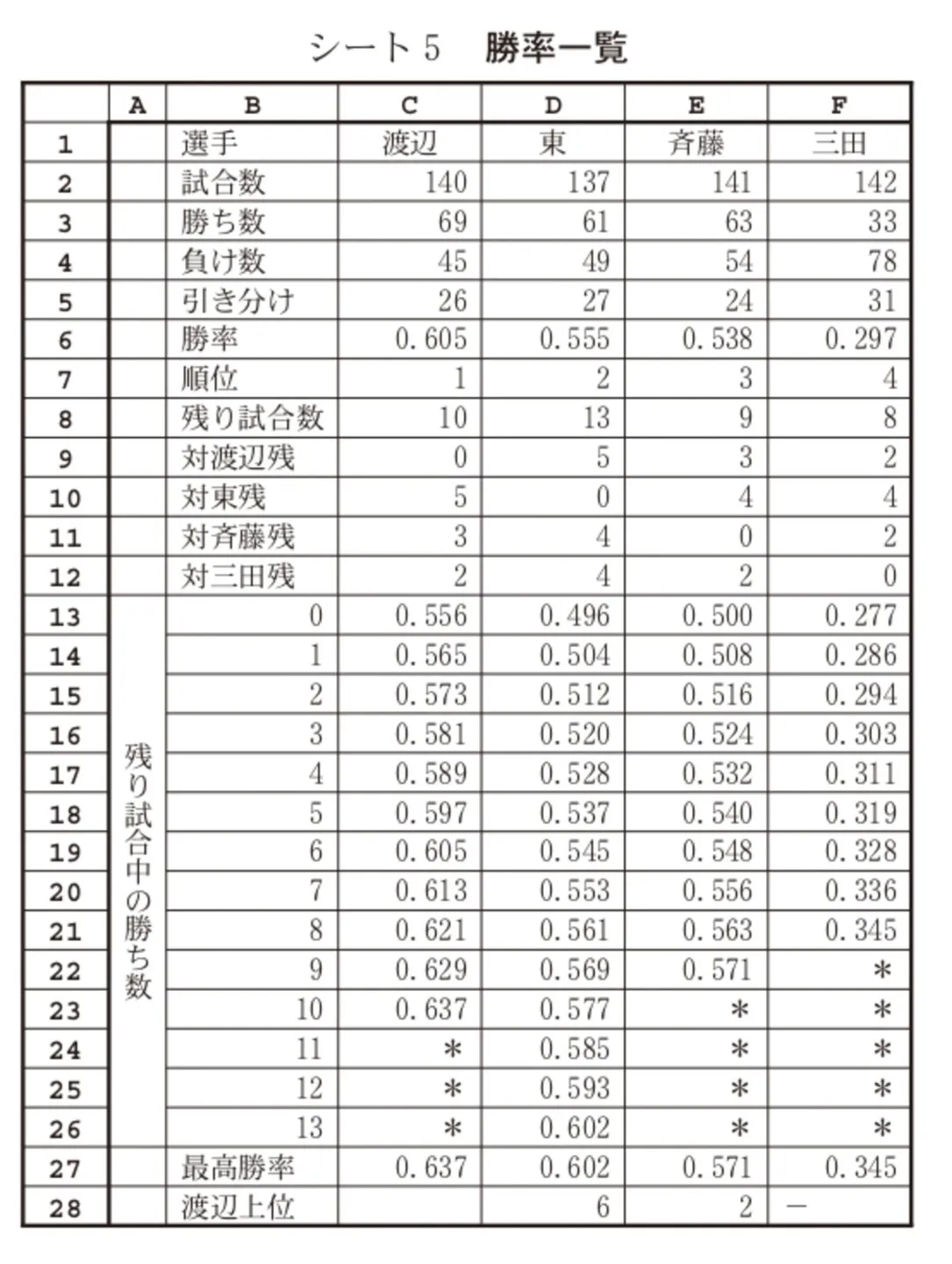
残り試合数が少なくなり、Nさんは、現在順位1位の渡辺選手が、残り試合のうち何勝すれば最終的に1位になるかを調べることにした。ただし、引き分けを含めた分析は複雑なので、引き分けを考えずに分析を進めた。シート2を拡張してシート5勝率一覧を作成し、残り試合中の勝ち数により各選手の勝率がどのように変化するかを表示した。
まず、8行目には各選手の残り試合数を表示した。9行目から12行目には各選手の他選手との残り試合数を表示した。例えば、セルC10は、渡辺選手と東選手との試合があと5試合残っていることを表す。また、セル範囲B13~B26は、残り試合中の勝ち数を表す。セル範囲C13~F26には、セル範囲B13~B26に対応させ、各選手の現在までの勝ち数と残り試合での勝ち数を合計した場合の勝率を表示した。例えば、セルC13は渡辺選手が残り試合を0勝10敗とした場合の勝率となる。また、残り試合数を超えている場合には「*」を表示する。そのために、セルC13に次の計算式を入力し、セル範囲C14~C26とセル範囲D13~F26に複写した。
IF(C$8<[ タ ],"*",(C$3+[ タ ])/(C$3+C$4+[ チ ]))
27行目には各選手が残り試合をすべて勝った場合の勝率を最高勝率として表示した。他選手の最高勝率を、渡辺選手の勝率が上回れば渡辺選手は確実に1位となる。28行目には、他選手の最高勝率を上回るために、渡辺選手が必要な勝ち数を表示する。ただし、渡辺選手が残り試合をすべて負けても、渡辺選手の勝率が上回る場合には「-」を表示する。ここで、検索条件として比較演算記号とセル番地を使用する場合には文字列として連結する必要があるので、"<="&D27と指定する。これらより、セルD28に次の計算式を入力し、セル範囲E28~F28に複写した。
IF(D27<[ ツ ],"-",COUNTIF([ テ ],"<="&D27))
完成したシート5を見直すと、( ト )ことや( ナ )ことがわかった。Nさんは、現状を把握でき、より関心をもって試合を観戦することができた。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
大学入学共通テスト(情報)試験 令和4年度(2022年度)本試験 問80(<旧課程>情報関係基礎(第4問) 問20) (訂正依頼・報告はこちら)
この競技を4人で競い合っている。各選手は他3人の選手と50試合(先攻25試合、後攻25試合)ずつ合計150試合、全体では300試合を行い、勝率により順位を決定する。勝率は、引き分けを除いた試合数で勝ち数を割って計算する。
次の文章を読み、空欄( ナ )に入れるのに最も適当なものを、後の解答群のうちから一つ選べ。なお、以下の問題を解答するにあたっては、使用する表計算ソフトウェアの説明(リンク) を参照するとよい。
残り試合数が少なくなり、Nさんは、現在順位1位の渡辺選手が、残り試合のうち何勝すれば最終的に1位になるかを調べることにした。ただし、引き分けを含めた分析は複雑なので、引き分けを考えずに分析を進めた。シート2を拡張してシート5勝率一覧を作成し、残り試合中の勝ち数により各選手の勝率がどのように変化するかを表示した。
まず、8行目には各選手の残り試合数を表示した。9行目から12行目には各選手の他選手との残り試合数を表示した。例えば、セルC10は、渡辺選手と東選手との試合があと5試合残っていることを表す。また、セル範囲B13~B26は、残り試合中の勝ち数を表す。セル範囲C13~F26には、セル範囲B13~B26に対応させ、各選手の現在までの勝ち数と残り試合での勝ち数を合計した場合の勝率を表示した。例えば、セルC13は渡辺選手が残り試合を0勝10敗とした場合の勝率となる。また、残り試合数を超えている場合には「*」を表示する。そのために、セルC13に次の計算式を入力し、セル範囲C14~C26とセル範囲D13~F26に複写した。
IF(C$8<[ タ ],"*",(C$3+[ タ ])/(C$3+C$4+[ チ ]))
27行目には各選手が残り試合をすべて勝った場合の勝率を最高勝率として表示した。他選手の最高勝率を、渡辺選手の勝率が上回れば渡辺選手は確実に1位となる。28行目には、他選手の最高勝率を上回るために、渡辺選手が必要な勝ち数を表示する。ただし、渡辺選手が残り試合をすべて負けても、渡辺選手の勝率が上回る場合には「-」を表示する。ここで、検索条件として比較演算記号とセル番地を使用する場合には文字列として連結する必要があるので、"<="&D27と指定する。これらより、セルD28に次の計算式を入力し、セル範囲E28~F28に複写した。
IF(D27<[ ツ ],"-",COUNTIF([ テ ],"<="&D27))
完成したシート5を見直すと、( ト )ことや( ナ )ことがわかった。Nさんは、現状を把握でき、より関心をもって試合を観戦することができた。

- 渡辺選手は、残り試合をすべて負けると最下位になる
- 渡辺選手は、残り試合のうち6勝すると1位になることが確実である
- 東選手は、残り試合をすべて勝つと1位になる
- 斉藤選手は、残り試合をすべて勝っても東選手の勝率を絶対に上回れない
- 三田選手は、残り試合をすべて勝つと1位になる
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
注意)
[ト]と[ナ]は順不同です。正しい答えを2つ選ぶ形式です。
解答は[ト]と[ナ]で同一のものですので気を付けてください。
順番に 選択肢を検討していきましょう。
[誤り]
渡辺選手の、残り試合をすべて負けた時の勝率は C13 セルの 0.556 です。
一方で、例えば三田選手の最高勝率は F27 の 0.345 です。これを比較すると、渡辺選手が勝っているといえますので、最下位ではありません。
[正しい]
渡辺選手が6勝した時点で、勝率は C19 の 0.605 となります。
他選手の最大勝率は D27 ~ F27 であり、いずれも 0.605 未満です。
ですから、6勝時点で1位となることは確実といえます。
[正しい]
東選手が残り試合をすべて勝利した場合の勝率は 0.602。
渡辺選手は、東選手に 5 試合分負けることになりますので、他選手にすべて勝ったとした場合の勝率は (残り試合のうち5試合勝利したときの) 0.597。
また、斎藤選手および三田選手は、0.602 を絶対に上回ることができません。(E27~F27)
よって、東選手が1位といえます。
[誤り]
斎藤選手が残り試合すべて勝った場合の勝率は E27 の 0.571。
東選手が、残り試合すべて負けた場合の勝率は D13 の 0.496。
斎藤選手の勝率が上回っています。
[誤り]
三田選手が残り試合すべて勝った場合の勝率は F27 の 0.345。
他選手について、残り試合すべて負けた場合の勝率は C13 ~ E13 の値により、すべて 0.345 を上回っています。
ですので、三田選手はどれだけ試合に勝ったとしても最下位となることがわかります。
参考になった数0
この解説の修正を提案する
前の問題(問79)へ
令和4年度(2022年度)本試験 問題一覧